Expectation and Sample Mean

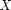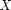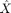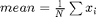For a certain distribution $X$, we know the expectation. If we get a sample of $X$, which we call it $\hat{X}$, we are also able to calculate the empirical average or mean of the sample, $mean = \frac{1}{N} \sum x_i$.

Contents

What's the relationship between empirical mean and theoretical expectation?

Uniform distribution example

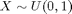$X \sim U(0, 1)$;

alpha1 = 0;
beta1 = 1;

Compute THEORETICAL values;

mean1 = (beta1 - alpha1) / 2;

Compute empirical values;

sizes = [5,10,50,100,500,1000,5000]; % For different sampling sizes;
nS = length(sizes);
mean2 = zeros(nS,1);
variance2 = zeros(nS,1);
for sizeIndex = 1:nS
    aSize = sizes(sizeIndex);
    ys = unifrnd(alpha1, beta1,[aSize,1]);
    mean2(sizeIndex) = mean(ys);
    variance2(sizeIndex) = var(ys);
end
fig1a = figure;
xlim([min(sizes) max(sizes)]);
ylim([0, max(mean2)]);
plot(sizes,mean2, '-r');
hold on;
plot(sizes,repmat(mean1,1,nS),'-b');
legend('EMPIRICAL','THEORETICAL');
title('Mean');

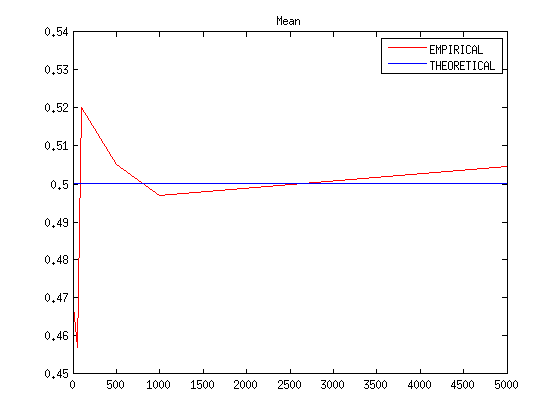
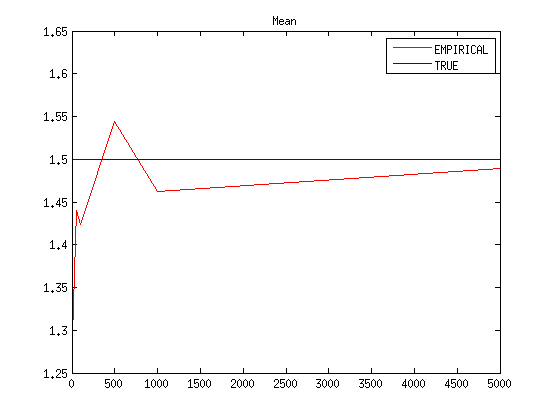
Pareto distribution example

Let's do the same for 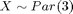$X \sim Par(3)$;

alpha1 = 3;
k1 = 1/alpha1;
sigma1 = 1/alpha1;
theta1 = 1;

Compute THEORETICAL values;

mean1 = alpha1/ ( alpha1 - 1);

Compute empirical values;

rep = 100;
sizes = [5,10,50,100,500,1000,5000];
nS = length(sizes);
mean2 = zeros(nS,1);
for sizeIndex = 1:nS
    aSize = sizes(sizeIndex);
    aMean = 0;
    ys = gprnd(k1,sigma1,theta1,[aSize,1]);
    mean2(sizeIndex) = mean(ys);
    variance2(sizeIndex) = var(ys);
end
fig1a = figure;
xlim([min(sizes) max(sizes)]);
ylim([0, max(mean2)]);
plot(sizes,mean2, '-r');
hold on;
plot(sizes,repmat(mean1,1,nS),'-b');
legend('EMPIRICAL','TRUE');
title('Mean');


Published with MATLAB® R2014a